Lý giải \"Nghịch lý ngày sinh nhật\"
Đăng 8 năm trướcNghịch lý ngày sinh nhật mới nghe thì rất khó tin. Tuy nhiên nó hoàn toàn có thể chứng minh bằng toán học.
Như đã hứa ở bài viết này trước đây, hôm nay tôi sẽ viết một bài lý giải về "Nghịch lý ngày sinh nhật".
Nghịch lý ngày sinh nhật được phát biểu như sau:
Nếu 23 người cùng ngồi trong một căn phòng, xác suất khoảng 50% có ít nhất 2 người có cùng ngày sinh nhật. Nếu căn phòng có 75 người thì xác suất này sẽ là 99,9%.
Sở dĩ gọi là nghịch lý bởi vì:
- Nó là sự thật.
- Nhưng lại nghe rất vô lý và phản trực giác.
Tính xác suất để trong 23 người có ít nhất 2 người có cùng ngày sinh nhật:
Giả định tất ả mọi người đều sinh vào năm thường (có 365 ngày). Nếu có người sinh vào năm nhận cũng không ảnh hưởng nhiều đến kết quả tính toán.
Xác suất để người thứ nhất có sinh nhật độc lập là 100%
Xác suất để người thứ hai có sinh nhật độc lập (tức là không trùng sinh nhật với người thứ nhất) là (365-1)/365 = 1 - 1/365
Tương tự, xác suất để người thứ ba có sinh nhật độc lập (tức là không trùng với 2 ngừoi đầu tiên) là 1 - 2/365
...........
Xác suất để người thứ 23 có sinh nhật độc lập (không trùng với 22 người đầu tiên) là 1 - 22/365.
Như vậy xác suất để tất cả mọi người không có ai trùng sinh nhật với nhau là:
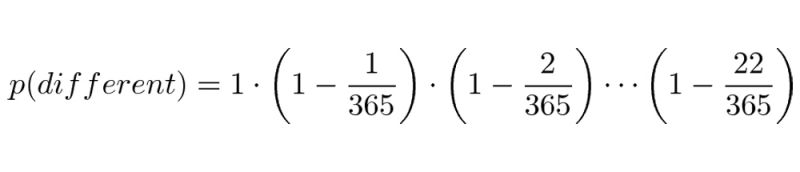
Tích số này trông khá khó nhằn. Tuy nhiên thật may mắn chúng ta có Định lý Taylor, khi x tiến gần tới 0 thì chúng ta có biểu thức sau:
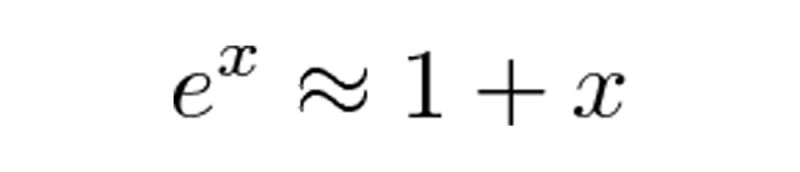
Cho nên:
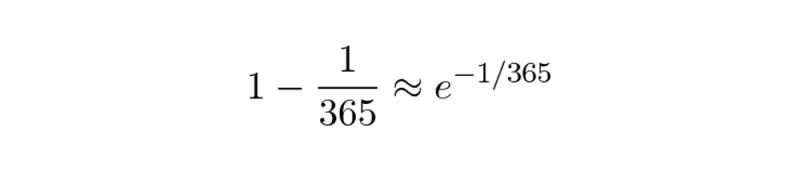
Áp dụng định lý Taylor vào tích số phía trên chúng ta có:
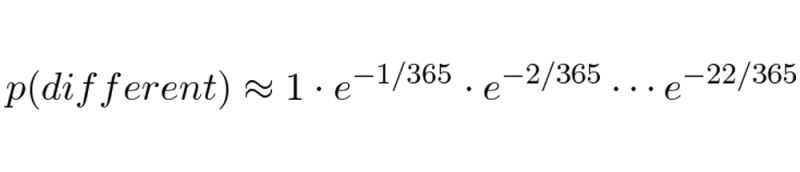
Và chúng ta biết rằng tổng các số tự nhiên liên tiếp từ 1 đến n bằng n (n + 1) / 2. Do đó tổng các số từ 1 đến 22 bằng 23.22/2. Áp dụng vào ta có:
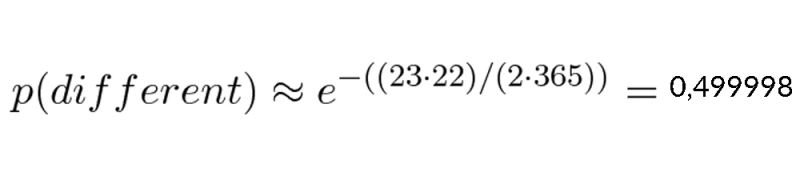
Vậy xác suất để có ít nhất 2 người trùng ngày sinh nhật = 1 - p(different) = 1 - 0,499998 = 0,500002.= 50%
Như vậy Nghịch lý ngày sinh nhật đã được chứng minh.
Tính tương tự với trường hợp 75 ngày cho ra kết quả 99,9%.

******************************
Các bài viết khác của tôi có thể bạn sẽ thích:
